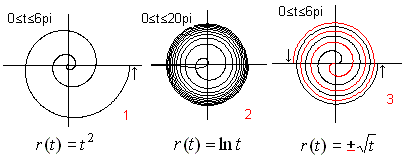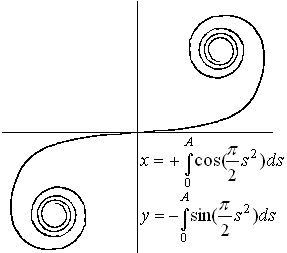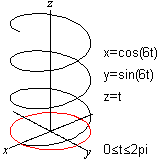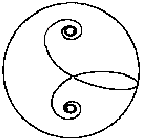सर्पिल क्या है?


एक सर्पिल विमान या अंतरिक्ष में एक वक्र है, जो एक विशेष तरीके से एक केंद्र के चारों ओर चलाता है।
विभिन्न सर्पिल का पालन करें। इनमें से ज्यादातर सूत्रों द्वारा निर्मित होते हैं।
ध्रुवीय समीकरण द्वारा सर्पिल शीर्ष
आर्किमिडीन सर्पिल
आप एक बिंदु के दो गति से एक सर्पिल बना सकते हैं: एक निश्चित दिशा में एक समान गति होती है और निरंतर गति से एक चक्र में एक गति होती है दोनों गति उसी बिंदु पर शुरू होती है।
(१) बाईं ओर एक समान गति एक बिंदु को दायीं ओर ले जाती है। – नौ स्नैपशॉट्स हैं
(२) एक स्थिर कोणीय वेग के साथ गति एक सर्पिल पर एक ही समय में बिंदु को स्थानांतरित करता है। – हर ८ वां मोड़ एक बिंदु है
(३) वक्र के रूप में एक सर्पिल आता है, यदि आप प्रत्येक मोड़ पर बिंदु बनाते हैं।
आप सर्कल समीकरणों के अनुरूप सूत्रों को प्राप्त करते हैं।
वृत्त
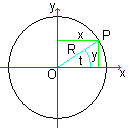
चलो पी त्रिज्या आर के साथ एक वृत्त का एक बिंदु हो, जो केंद्र की स्थिति में एक समीकरण द्वारा दिया गया है।
सर्कल के तीन आवश्यक विवरण हैं:
(१) केंद्रीय समीकरण: x²+y² = R² or [y = sqr(R²-x²) und y = -sqr(R²-x²)],
(२) पैरामीटर फॉर्म: x(t) = R cos(t), y(t) = R sin(t),
(३) ध्रुवीय समीकरण: r(t) = R
आप (सरल) ध्रुवीय समीकरण में एक जोड़ी (त्रिज्या ओपी, कोण टी) के द्वारा एक बिंदु दें। त्रिज्या उत्पत्ति (0 | 0) से बिंदु की दूरी है। कोण त्रिज्या और सकारात्मक एक्स-अक्ष के बीच स्थित है, इसकी उत्पत्ति मूल में है।
कुंडली
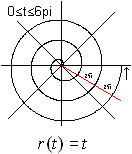
त्रिज्या r (t) और कोण टी सरलीकृत सर्पिल के लिए आनुपातिक हैं, आर्किमिडीज के सर्पिल। इसलिए समीकरण है:
(३) ध्रुवीय समीकरण: r(t) = at [ a स्थिर है]
इस प्रकार से
(२) पैरामीटर फॉर्म: x(t) = at cos(t), y(t) = at sin(t),
(१) केंद्रीय समीकरण: x²+y² = a²[arc tan (y/x)]²
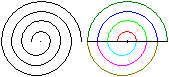
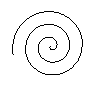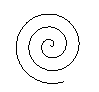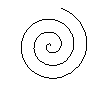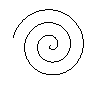
आर्किमिडीन सर्पिल मूल में शुरू होता है और तीन राउंड के साथ एक वक्र बनाता है।
सर्पिल शाखाओं के बीच की दूरी एक समान है।
अधिक सटीक: मूल के माध्यम से एक रेखा के साथ प्रतिच्छेदन बिंदुओं की दूरी समान होती है।
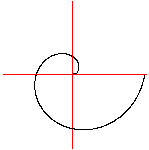
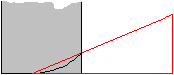
यदि आप एक सीधी रेखा पर एक आर्किमिडीज सर्पिल को प्रतिबिंबित करते हैं, तो आपको विपरीत दिशा के साथ एक नया सर्पिल मिलता है।
दोनों सर्पिल बाहर जाना है यदि आप सर्पिल को देखते हैं, तो बायी ओर एक बाईं तरफ जा रहा वक्र बनाता है, सही दाएं दाईं ओर जा रहा वक्र बनाता है।
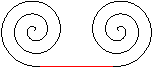
यदि आप सीधे (लाल) या घुमावदार वक्र से दोनों सर्पिल जोड़ते हैं, तो एक डबल सर्पिल विकसित होता है।
समनुरूप सर्पिल (लॉगरिदमिक सर्पिल, बर्नोली की सर्पिल)
(1) ध्रुवीय समीकरण: r(t) = exp(t)
(2) पैरामीटर फॉर्म: x(t) = exp(t) cos(t), y(t) = exp(t) sin(t)
(3) केंद्रीय समीकरण: y = x tan[ln(sqr(x²+y²))].
लॉगरिदमिक सर्पिल भी बाहर चला जाता है।
सर्पिल में एक विशिष्ट विशेषता है: मूल (लाल) में शुरू होने वाली प्रत्येक पंक्ति उसी कोण के साथ सर्पिल को घटा देती है।
अधिक सर्पिल
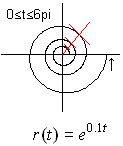
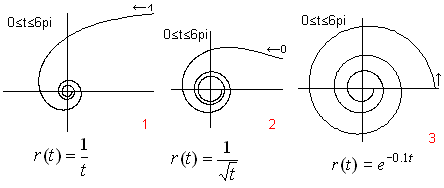
यदि आप आर्किमेडियन सर्पिल के दूसरे शब्दों से r (t) = at शब्द की जगह लेते हैं, तो आप कई नए सर्पिल प्राप्त करते हैं छह सर्पिल हैं, जो आप फ़ंक्शन f(x) = x ^ a [a = २,१/२, -१/२, -१] और f (x) = exp (x), f के साथ वर्णन कर सकते हैं ( x) = ln (x)। आप दो समूहों को अलग-अलग समझते हैं कि पैरामीटर 0 से कैसे बढ़ता है।
अगर फ़ंक्शन r (t) का पूर्ण मापांक बढ़ता जा रहा है, तो सर्पिल अंदर से बाहर की ओर चलते हैं और सभी सीमाओं से ऊपर जाते हैं।
सर्पिल १ परवलयिक सर्पिल या फ़र्मट सर्पिल कहा जाता है।
यदि फ़ंक्शन r (t) के पूर्ण मापांक कम हो रहा है, तो सर्पिल बाहर से बाहर की ओर चलती है। वे आम तौर पर केंद्र तक जाते हैं, लेकिन वे इसे तक नहीं पहुंचते हैं एक पोल है।
सर्पिल २ को लितुस (कुटिल स्टाफ) कहा जाता है।
मैंने प्लॉटिंग के लिए उपयुक्त विभिन्न सर्पिल फ़ार्मुलों के लिए समीकरण चुना। कर्मचारी)।
क्लॉइडियाड (कॉर्नू स्पायरल)
क्लॉइडॉयड या डबल सर्पिल एक वक्र है, जिसका वक्रता उत्पत्ति से दूरी के साथ बढ़ता है। वक्रता का त्रिज्या उत्पत्ति से मापा अपने चाप के अनुपात के विपरीत है।
पैरामीटर फॉर्म में दो समीकरण होते हैं, जो फ़्रेस्नेल के एन्फैनल के साथ होते हैं, जिसे केवल लगभग हल किया जा सकता है।
लहर सिद्धांत में एक एकल भट्ठा पर फ्रेसनेल के विवर्तन के ऊर्जा वितरण का वर्णन करने के लिए आप कोर्नु सर्पिल का उपयोग करते हैं।
सर्पल्स मेड ऑफ आर्क्स
हाफ सर्कल सर्पिल
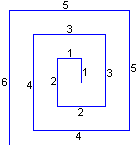
आप सर्पिल प्राप्त करने के लिए कदम से कदम बढ़ते हुए आधे हलकों को जोड़ सकते हैं।
त्रि-रे अनुपात १:१.५:२:२.५:३ …..
फिबोनैचि सर्पिल
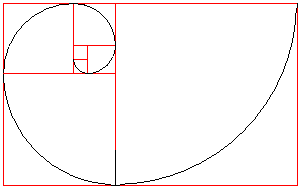
एक-दूसरे के शीर्ष पर दो छोटे वर्ग बनाएं बढ़ते वर्गों के एक क्रम को घड़ी की दिशा में जोड़ें।
वर्गों (काला) के अंदर तिमाही हलकों को आकर्षित करें।
वे फिबोनैचि सर्पिल बनाते हैं।
फिबोनैपी सर्पिल को इसकी संख्या के बाद कहा जाता है। यदि आप क्रम में चौकोर पक्षों की लंबाई लेते हैं, तो आप अनुक्रम १,१,२,३,५,८,१३,२१प्राप्त करते हैं … ये फिबोनाची संख्याएं हैं, जिन्हें आप रिकर्सिव फॉर्मूला से पा सकते हैं a(n)=a(n-1)+a(n-2) with [a(1)=1, a(2)=1, n>2].
रेखा सेगमेंट के बने सर्पिल
सर्पिल रेखा खंडों द्वारा १,१,२,२,३,३,४,४ लंबाई के साथ बनाया जाता है ….
लाइन्स एक दूसरे को सही कोण पर मिलते हैं।
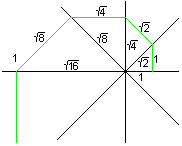
क्रॉसिंग में एक सर्पिल को चार सीधा रेखाओं को छेदने के साथ खींचें, जो ४५ डिग्री कोण बनाते हैं। क्षैतिज रेखा १ के साथ शुरू करें और सीधी रेखा के लिए लंबवत पंक्ति को अगली पंक्ति से मोड़ो। लाइन खंड सामान्य अनुपात वर्ग (२) के साथ एक ज्यामितीय क्रम बनाते हैं।
यदि आप एक सीधी रेखा बंडल में सर्पिल आकर्षित करते हैं, तो आप लॉगरिदमिक सर्पिल से संपर्क करते हैं, यदि कोण छोटे और छोटे होते हैं।
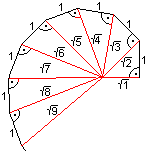
अगले सर्पिल को सही कोण त्रिकोण की एक श्रृंखला से बनाया जाता है, जिसमें एक आम पक्ष है एक त्रिकोण का कर्ण कर्ण अगले के पैर बन जाता है पहला लिंक १-१-एसक्यूआर (२) – त्रिकोण है
मुक्त पैर सर्पिल के रूप में
यह विशेष है कि रेखा खंडों में त्रिकोण स्पर्श। उनकी लंबाई प्राकृतिक संख्याओं की जड़ है आप पाइथागॉरियन प्रमेय के साथ इस सबूत कर सकते हैं।
इस आकृति को रूट सर्पिल या रूट घोंघा या थियोडोरस का पहिया कहा जाता है।
चौराहों को उनके केंद्र के चारों ओर १० डिग्री के साथ बदल दिया जाता है और एक ही समय में संकुचित होता है, ताकि उनके कोने अपने पूर्ववर्ती वर्ग के किनारे बने रहें।
परिणाम: कोनों चार सर्पिल हथियार बनाते हैं। सर्पिल लघुगणक सर्पिल के समान है, अगर कोण छोटे और छोटे होते हैं
आप अन्य नियमित बहुभुजों को भी बदल सकते हैं उदा। एक समभुज त्रिभुज आपको समान आंकड़े मिलते हैं।
यह तस्वीर मुझे कंप्यूटिंग के प्रारंभिक दिनों (सी ६४-नॉस्टलैगिया) की प्रोग्रामिंग भाषा लोगो की याद दिलाती है।
त्रि-आयामी सर्पिल
कुंडलित वक्रता
यदि आप x = cos (t) और y = sin (t) के साथ एक चक्र खींचते हैं और इसे z- दिशा में समान रूप से खींचते हैं, तो आपको बेलनाकार सर्पिल या हेलिक्स नामक एक स्थानिक सर्पिल मिलता है।
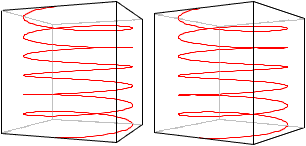
चित्र जोड़ी एक ३डी दृश्य को संभव बनाता है।
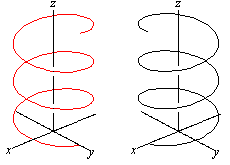
एक ऊर्ध्वाधर विमान पर ३डी -सर्पिल को प्रतिबिंबित करें आपको विपरीत दिशा के साथ एक नया सर्पिल (लाल) मिलता है।
यदि आप दायां सर्पिल के चारों ओर अपने दाहिने हाथ को पकड़ते हैं और यदि आपका अंगूठे सर्पिल अक्ष की दिशा में इंगित करता है, तो सर्पिल दक्षिणावर्त ऊपर की ओर चलता है। यह सही परिपत्र है।
बाएं सर्पिल के लिए आपको अपने बाएं हाथ का उपयोग करना चाहिए यह परिपत्र छोड़ दिया है रोटेशन घड़ी की घड़ी के विपरीत है।
उदाहरण: लगभग सभी शिकंजा एक दक्षिणावर्त रोटेशन हैं, क्योंकि अधिकांश लोग दायां हाथ रखते हैं।
“तकनीकी” साहित्य में सही परिपत्र सर्पिल को इस प्रकार समझाया गया है: आप एक सिलेंडर के चारों ओर दायां कोण वाले त्रिभुज को हवा देते हैं एक दक्षिणावर्त घूर्णन सर्पिल विकसित होता है, यदि त्रिकोण दायीं ओर बढ़ जाता है।
शंक्वाकार हेलिक्स
आप आर्किमिडीन सर्पिल या समकोण सर्पिल के साथ शंकु हेलिक्स बना सकते हैं।
चित्र जोड़े ३डी दृश्यों को संभव बनाते हैं।
लोक्सोड्रोम, गोलाकार हेलिक्स
लॉक्सोड्रोम क्षेत्र पर एक वक्र है, जो निरंतर कोण पर मेरिडियन को काटता है। वे मर्केटर प्रक्षेपण पर सीधी रेखा के रूप में दिखाई देते हैं।
पैरामीट्रिक प्रतिनिधित्व है।
x=cos(t) cos [1/tan (at)]
y=sin(t) cos[1/tan (at)]
z= -sin [1/tan (at)] (a स्थिर है)
आप ढूंढ सकते हैं x²+y²+z²=1. इस समीकरण का अर्थ है कि लॉक्सोड्रोम क्षेत्र पर झूठ बोल रहा है।
आम तौर पर एक अक्ष के बारे में रोटेशन द्वारा बनाई गई प्रत्येक ठोस पर एक लोक्सोड्रोम है।
सर्पिल बनाना
कागज की एक पट्टी एक सर्पिल बन जाती है, यदि आप अंगूठे और चाकू के किनारे के बीच की पट्टी खींचते हैं, तो कड़ी मेहनत सर्पिल एक कर्ल बन जाता है जहां गुरुत्वाकर्षण मौजूद है।
आप सिंथेटिक सामग्री के छोर को सजाने के लिए इस आशय का उपयोग करते हैं, जैसे उपहार-लपेटने में प्रयुक्त संकीर्ण रंगीन स्ट्रिप्स या रिबन।
मुझे लगता है कि आपको इस आशय को एक बाईमेटेलिक बार के रूप में समझा जाना है आप दो स्ट्रिप्स के साथ एक बृहदान्त्र बार बनाते हैं, प्रत्येक एक अलग धातु से बने होते हैं। एक बार इस बाईमेटेलिक बार को गरम किया जाता है, एक धातु की पट्टी दूसरे से अधिक फैलती है जिसके कारण बार को मोड़ना पड़ता है।
कारण है कि कागज झुकता की पट्टी शीर्ष और नीचे की ओर के बीच के तापमान में अंतर के साथ ऐसा करने के लिए बहुत ज्यादा नहीं है। चाकू पेपर की सतह की संरचना को बदलता है। यह तरफ ‘छोटा’ हो जाता है
संयोग से, यदि आप मोमबत्ती लौ की गर्मी में पकड़ते हैं तो कागज की एक पट्टी थोड़ा मोड़ लेती है।
कर्ल बनाने से मुझे एक पुराने बच्चों के खेल की याद दिलाता है: डंडेलाइंस फूल ले लो और स्टेम को दो या चार स्ट्रिप्स में कट कर सिर को बरकरार रखें। यदि आप फूल को कुछ पानी में डाल देते हैं, जिससे सिर सतह पर तैरता है, स्टेम की स्ट्रिप्स को कर्ल कर देगा। (स्पॉट मन।)
एक संभावित स्पष्टीकरण: शायद स्ट्रिप्स के प्रत्येक तरफ पानी के अलग-अलग अवशोषण के कारण उन्हें कर्ल लगाया जा सकता है।
मंडलब्रॉट सेट सर्पिल
निर्देशांक चित्रों के केंद्र से संबंधित हैं।
जूलिया समूह के रूप में आपको अच्छा बढ़ता है यहाँ एक उदाहरण है:
Image
मेरे पृष्ठ पर इन ग्राफिक्स के बारे में आपको अधिक जानकारी मिलती है मंडेलब्रॉट सेट।
सर्पिल मेड ऑफ़ मेटल
आपको बाड़ वाली खिड़कियां, बाड़, द्वार या दरवाजों की सजावट के रूप में अच्छा बढ़ता है। आप उन्हें हर जगह देख सकते हैं, अगर आप चारों ओर देख रहे हैं।
मुझे नई उल्म, मिनेसोटा, संयुक्त राज्य अमरीका में प्रदर्शित करने के लिए लायक सर्पिल मिला।
जर्मन वंश के अमेरिकियों ने १९०० में डेटमॉल्ड / जर्मनी के पास हरमन स्मारक की एक प्रति का निर्माण किया।
कई सर्पिल के साथ लोहे की रेलिंग सीढ़ियों (फोटो) को सजाने के लिए।
विकिपीडिया पृष्ठों पर अमेरिकी और जर्मन हरमन के बारे में अधिक जानकारी (नीचे यूआरएल)
कॉस्टयूम गहने भी मकसद के रूप में बढ़ते हैं।
एनेट के सर्पिल
सर्पिल, स्पायरल, स्पिरल
अम्मोनी, जंगली भेड़ के शंकु, आर्किमिडीज के जल सर्पिल, उच्च या निम्न दबाव का क्षेत्र, सूरजमुखी के कोर का क्षेत्र, बैमेटल थर्मामीटर, बिशप स्टाफ, ब्रिटनी साइन, सागर-ईगल के मंडल, चढ़ते हैं, दक्षिणावर्त घूमते लैक्टिक एसिड, धुआं, कुंडली, कुंडल वसंत, कॉर्क सक्वेर, लुगदी (पौधों), कर्ल, मौसम विज्ञान में अवसाद, बल्ब की डबल फिलामेंट, डीएनए का डबल हेलिक्स, डबल सर्पिल, चुंबकीय अनुदैर्ध्य क्षेत्र में इलेक्ट्रॉन किरण, इलेक्ट्रॉन साइक्लोट्रोन, एक्सर सर्पिल, फिंगर मार्क, फ़िर कोन, ग्लाइडर चढते हुए, एक रिकार्ड की नाली, संगीत वाद्य वायलिन के प्रमुख, हॉटप्लेट, गर्मी सर्पिल, जड़ी बूटी सर्पिल, मुद्रास्फीति सर्पिल, टेडपोल की आंत, ज्ञान सर्पिल, लैलासीस घोंघे, जीवन सर्पिल, लोरेनज़ अटेरकोर, समररा (इराक) में मीनार, गैलीलली पेंडुलम के पेंडुलम बॉडी, रोम में ट्राजन कॉलम की राहत पट्टी या हिल्डेशम में बर्र्नवर्ड कॉलम, चट्टानी घोंघे, एक शंकु पर्वत की सड़क , भूमिका (तार , धागा, केबल, नली, टेप माप, कागज, पट्टी), पेंच धागे, घर्षण के साथ सरल पेंडुलम, आराम की स्थिति में साँप, एस्क्यूलेपियस का साँप, इंटीरियर कान, स्क्रॉल, स्क्रू एल्गा, घोंघे-शेल, स्पाइडर नेट, सर्पिल व्यायाम किताब, सर्पिल नेबुला, सर्पिल सीढ़ी (जैसे बर्लिन में रिक्स्टाग के गिलास गुंबद में दो सर्पिल सीढ़ियाँ), स्पायरलला ;-), स्पायरली नूडल्स, स्पाइरिलस (जैसे कि क्लेरा बेसीलस), एक गद्दे के स्प्रिंग्स, गोभी सफेद तितली का सक्शन ट्रंक (निचला जबड़ा), की पूंछ समुद्री घोड़े, कॉनिफ़र, जीभ और चामलेयन की पूंछ, सीडी या डीवीडी पर निशान, तिगुनी चुरा, दिग्गजों के दाग, वायरस, वाल्ट, घड़ी के झरने और मैकेनिकल घड़ियां, भँवर, बवंडर का संतुलन वसंत।